Celebrating Pi - A Transcendental Number

Celebrating Pi – A Transcendental Number

Posted March 11, 2016

The most beautiful thing we can experience is the mysterious. It is the source of all true art and science.”

– Albert Einstein

As an educator, I like to find as many reasons to celebrate knowledge as possible. So when I learned that March 14th is internationally recognized as Pi Day – because that date is 3/14, as the rounded pi number 3.14 – I was a little perplexed, to be quite honest. Why is a simple number being celebrated by so many people?

Sure, it’s always a good time to eat pie in school, which many educators already do every Pi Day. Most people are familiar with pi as the constant π derived from dividing the circumference by the radius of any circle. Pi helps us find the circumference and the area of circles; that’s useful. But is that all pi is good for – circles and a reason to delight in some delicious pies?

Dear reader, you’ll want to take a moment and brace yourself for this.

In mathematical calculations, we often use the shortened 3.14 instead of the irrational and infinite string of digits that π rebelliously is. Did you know it has over 1 trillion digits after the decimal point? Thanks to the invention of the computer (which stemmed from the root word compute because it performs calculations), mathematicians could get that far. However, they are still trying to find the next unpredictable digit in the sequence. Just as a teaser, here are the first 500 digits for you:

Facts About Pi

Before I give educators any ideas for pi-inspired activities to do with their learners, let me tell you a few amazing facts about pi that will be sure to enlighten you in a way no number ever has.

One doesn’t need to be a physician in signal processing to appreciate the usage of a cell phone. You should know that when your cell communicates with the local cell tower, it performs something called a Fourier transform. The equation for the Fourier transform is this:

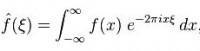(Yes, that’s right. The value of π lives on in the innermost workings of your smartphone, somewhere, somehow.)

As human beings, we deal with the world on a large scale, often without knowing what is happening on an atomic and subatomic level. Frankly, we don’t always need to know how particles behave to live fulfilling lives. But many scientists do care and want to understand why things are the way they are, from the smallest possible details, and here is where quantum mechanics comes in. Quantum mechanics is the science of relating to the very small. In it, there is something called a Schrodinger equation, which describes how the wave function of a physical system evolves, represented as:

(Notice anything familiar? Intriguing, isn’t it.)

I’ll casually throw in one more mathematical equation about the General Theory of Relativity. Einstein’s “field equations” describe the gravitational effects produced by a given mass, represented as:

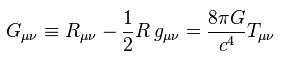(Do you see what I see? Alas, it is π once more, creeping in here and there in unexpected ways. It’s everywhere!)

Could pi be a part of the universe’s fabric itself?

Celebrate Pi Day in Your Classroom

I could go on, but I think this is enough to spark your amazement at how a commonly used number like π is so incredibly mysterious. It’s enough of a reason to have an international Pi Day! And so, if you want some ideas on how to celebrate it with your learners in an educational manner (worry not, this does not replace the pie-eating component), here are a few suggestions:

Have learners measure circular objects in the classroom & calculate an experimental value for pi. You can use a string to measure the circumference and then align it to a ruler for the actual measurement before dividing the circumference over the diameter of each object. Don’t tell them what the theoretical value should be. Let them discover the pattern on their own!

Learners can experimentally find the value of π by graphing a line of best fit, calculating for the slope to find pi. Let them plot several coordinate points, with x being the diameter and y being the circumference. It is an opportune moment to bring linear regression lines and correlation coefficients to life!

Since the first six values of pi are 3.14159, on 3/14, at exactly 1:59 PM, sing a song about pi or make up your own!

Work on percentages by asking learners to solve a problem finding the percent increase in the area of a circular edible thing (pizza or pie) if the radius increases from 22 to 25 centimetres.

Talk about Albert Einstein!

You may be wondering, why should we talk about Einstein on this particular day? Besides the fact that pi is found in the Einstein field equations, suffice to say that Einstein was born on Mar.14, 1879. That’s right, folks: coincidentally, Pi Day falls on Einstein’s birthday.

Share the joy that only comes from celebrating the transcendental number pi.

Have a lovely Pi Day!

—–